Prethodno poglavlje | Pocetna strana | Sledece poglavlje

 

 

8. UPRAVLJANJE ROBOTIMA

 

U glavi 3. opisali smo pogonske sisteme koji se koriste za pokretanje robota. U glavama 6. i 7. objasnili smo različite senzore koji čine takozvana čula. Priro­dan nastavak ovih razmatranje je definisanje sistema koji će obezbediti da robotski uređaj, opremljen čulima i pokretačkim sistemom, ostvari željeno kretanje sa kraj­njim ciljem izvršenja nekog postavljenog zadatka. To bi u najkraćem bio problem upravljanja robotom i sinteze upravljačkog sistema.

 

8.1. OPŠTI STAVOVI O UPRAVLJANJU ROBOTIMA

 

Razmotrićemo prvo pojam upravljanja u slučaju robotskog sistema, zatim nivoe upravljanja kao i neke pojmove značajne za primenu robota. Konačno, diskutovaćemo i o osnovnim tipovima upravljanja koji slede iz vrste postavljenog za­datka.

 

8.1.1.  Pojam i nivoi upravljanja

 

U glavi 3. o pogonskim sistemima definisali smo upravljačke promenljive pojedinih vrsta pogona. U slučaju elektromotora jednosmerne struje u pitanju je napon na motoru, a u slučaju elektrohidrauličnog pogona, struja servorazvodnika. Sada zadatak upravljanja možemo definisati na sledeći način: Obezbediti takvu promenu upravljačkih veličina koja će proizvesti zadato kretanje u zglobovima ro­bota. Dakle, zadatak se svodi na zadato pokretanje zglobova.

 

Ovakva definicija, međutim, često nas ne može zadovoljti. Radi se o tome da robot treba da vrši takozvano funkcionalno kretanje. Kako se funkcionalno kretanje, po pravilu, vezuje za završni uređaj robota, to zadatak upravljanja treba unekoliko preformulisati: Potrebno je obezbediti takvu promenu upravljačkih promenljivih koja će proizvesti traženi funkcionalni pokret, tj. traženo kretanje završnog uređa­ja u prostoru. Svakako, ovako formulisan upravljački problem uključuje i prethodnu definiciju. Naime, funkcionalni pokret treba raspodeliti na zglobove, a zatim zglo­bove pokrenuti.

 

Problem upravljanja robotom možemo postaviti još opštije. Umesto da za­datak formulišemo preko određenog  kretanja, možemo napraviti kvalitativni skok i zadatak formulisati u vidu zahteva da robot izvrši neku složenu praktičnu opera­ciju. Na primer, zadatak može biti: zavrnuti zavrtanj u predviđeni otvor. Ovakav zadatak sadrži niz funkcionalnih pokreta. Prvi pokret hvatanja zavrtnja, drugi prinošenje zavrtnja otvoru, treći zavrtanje i četvrti povratak u polazni položaj. Za­datak bi mogao biti još složeniji ako je, na primer, potrebno sastaviti neki sklop od više delova. Tada bi i broj elementarnih funkcionanih pokreta bio znatno veći. Konačno, veoma čest problem ovog tipa je sakupljanje predmeta rasutih po podlozi.

 

Opisani način postavljanja zadatka predstavlja kvalitativni skok u odnosu na ranije zahteve. Zadatak više nije kinematički orijentisan (zadato kretanje) već problemski orijentisan (izvršenje određene radnje). Problem koji treba rešiti ro­bot prvo raščlanjuje na elementarne zahvate, tj. na niz elementarnih funkcionalnih pokreta, a zatim ih izvršava. Očigledno, ovo raščlanjavanje problema i utvrđivanje redosleda elementarnih radnji zahteva određenu "inteligenciju" kao i određene in­formacije tj. odgovarajuća čula. Sada zadatak upravljanja može da se formuliše na sledeći način: analizirati, a zatim izvršiti traženu radnu operaciju.

 

U prethodnoj diskusiji podrazumevali smo rad u potpuno poznatim uslovima. Tu mislimo na precizno definisan radni prostor i radne operacije. Sledeće uopštenje predstavlja uvođenje veće doze neizvesnosti. Radi se, često, o pojavi prepreka u radnom prostoru. Izvršenje zadatka tada podrazumeva i stalno ispitivanje prostora oko robota i odlučivanje o tome kako u konkretnom slučaju postupiti da bi se izvršio zadatak. Formulacija zadatka upravljanja, ipak, ostaje ista kao malopre.

 

Na kraju, možemo zamisliti i naredno uopštenje: ne mora biti zadata čak ni radna operacija koju treba izvršiti. Postavimo, na primer, ovakav zadatak: Ispitati dati uređaj (ili sklop), naći kvar i otkloniti ga. U ovom slučaju robot će tek nakon analize zaključiti koje radne operacije treba izvršiti (npr. zameniti neki deo). Ovo uopštenje bi predstavljalo novi kvalitativni skok jer zadatak postaje orijentisan ka cilju i problem upravljanja formulišemo na odgovarajući način: izvršiti operacije potrebne da bi se postigao traženi cilj.

 

 

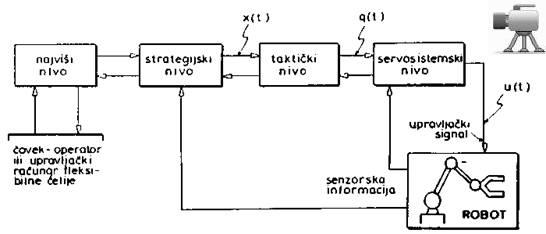
Sl. 8.1. Nivoi upravljačkog sistema

 

Sledeći opisanu logiku uopštavanja zadatka koji se robotu postavlja dolazimo do upravljanja u više nivoa (Sl.8.1.) pri čemu svaki viši nivo priprema zadatak i upravlja radom nižeg nivoa. Takođe, svaki nivo će, u zavisnosti od potrebe, raspolagati određenim senzorskim informacijama.

 

 Servosistemski nivo predstavlja najniži nivo upravljanja i on neposredno izvr­šava kretanje. Zato se, često, i naziva izvršni nivo. Zadatak mora biti u obliku zah­teva za određenim kretanjem zglobova: q(t), gde je q vektor unurašnjih koordinata. Servosistemi u svakom zglobu obezbeđuju izvršavanje traženog kretnja.

 

Ovaj upravljački nivo prima zadatak od višeg nivoa ili pak, neposredno od čoveka-operatora ako viši nivo ne postoji.

 

Od mogućih senzorskih informacija servosistemski nivo koristi podatke o položaju i brzini pomeranja zglobova.

 

Taktički nivo je prvi viši nivo upravljanja i on vrši raspodelu kretanja na pod-sisteme zglobova. Zadatak se prima od višeg nivoa ili čoveka-operatora neposredno i to u obliklu zahteva za izvršenje određenog funkcionalnog pokreta X(t), gde je X vektor spoljašnjih koordinata. Na ovom nivou rešava se inverzni zadatak kine-matike čime se nalaze kretanje zglobova q(t). Taktički nivo u principu ne zahteva dopunske senzorske informaije.

 

Strategijski nivo. Na ovom upravljačkom nivou, problemski orijentisan zada­tak (formulisan u obliku zahteva za izvršenja određene radne operacije) raščlanjuje se na elementarne funkcionalne pokrete X(t). Pri tome je neophodno izvršiti i pla­niranje kretanja koje nekada uključuje i različite vrste optimizacije koja omogućava da se raščlanjavanje izvrši na jednoznačan način. Na primer: treba po nekom kriterijumu optimizirati redosled sakupljanja rasutih predmeta. Strategijski nivo često uključuje vizuelne sisteme, daljinare i sl. Problem obilaženja prepreka u radnom prostoru može se rešavati na strategijskom nivou ili ga prepustiti sledećem višem nivou.

 

Najviši nivo upravljanja prima zadatak orijentisan ka cilju, analizira ga, i formuliše radne operacije potrebne za njegovo postizanje.

 

Na kraju ove diskusije treba naglasiti da se većina današnjih robota zadržava na taktičkom nivou, mada se intenzivno razvijaju metode veštačke inteligencije koje omogućavaju realizaciju strategijskog nivoa. Ovakvi inteligentni sistemi, mada postoje, još su srazmerno retki u odnosu na prostije robotske sisteme.

 

U nastavku ove glave obrađivaćemo prvenstveno najniži (servosistemski) nivo upravljanja. Naime, inverzni problem kinematike (traktički nivo) razmatran je u glavi 2, a viši nivoi se zasnivaju na metodama veštačke inteligencije, o čemu govori glava 9.

 

8.1.2. Preciznost kretanja

 

Preciznost kretanja robota je jedan od ključnih faktor uspešnog rada. Da bismo ovaj pojam bolje objasnili razmotrićemo tri veličine kojima se on u robotici opisuje: prostornu rezoluciju, tačnost pozicioniranja i ponovljivost. Sve ove veličine definisaćemo u odnosu na zadatak postizanja zadatog položaja robota u prostoru.

 

Prostorna rezolucija je najmanji pomeraj koji robot može izvršiti po nalogu upravljačkog sistema. To nam ukazuje da robot nema mogućnost kontinualnog po­zicioniranja, već postoji skup diskretnih položaja u radnom prostoru u koje robot možemo dovesti. Ova diskretizacija posledica je digitalizacije podataka o položaju u memoriji upravljačkog sistema. Na primer, ako se jedna unutrašnja koordinata pamti u obliku 8-bitne informacije, to znači da će ta koordinata imati 28=256 dis­kretnih položaja. Na slici 8.2a predstavljen je jedan deo diskretizovane koordinate .Dopunski problem javlja se usled mehaničkih efekata koji doprinose smanjenju mogućnosti tačnog pozicioniranja. Jedan od takvih efekata je zazor u prenosnom sistemu, drugi je elastična deformacija elemenata prenosnog sistema, a postoji još niz faktora koji pojačavaju ove efekte. Tako dolazimo do situacije da posmatrani zglob q^ ne možemo pozicionirati tačno u neku od diskretnih tačaka već će se koor­dinata naći negde u šrafiranoj okolini diskretizacionih tačaka (sl. 8.2a). Granice štafiranog intervala određuju se po metodi najgoreg slučaja uzimajući u obzir zbirni uticaj pomenutih mehaničkih faktora.

 

 

 

 

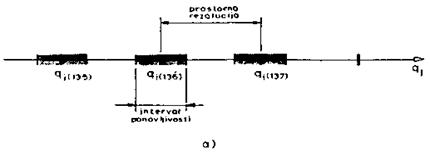
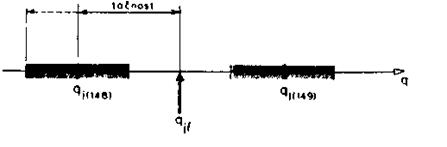
b)

 

SI. 8.2. Prostorna rezolucija, ponovljivost i tačnost

 

Ponovljivost opisuje sposobnost robota da ostvari položaj koji mu odredi up­ravljački sistem. Jasno je da to može biti samo neka od diskretizacionih tačaka. Kako smo već naglasili, usled mehaničkih nepreciznosti robot će doći u neki od položaja unutar šrafiranog intervala, pri čemu će pri svakom novom dolasku zauzeti drugi položaj iz intervala. Zato šrafirani interval na sl.8.2a nazivamo interval ponovljivosti. Eksperimentalno je moguće utvditi raspodelu verovatnoće zauzimanja pojedinih tačaka u intervalu ponovljivosti.

 

Tačnost pozicioniranja. Do sada smo razmatrali mogućnost robota da zauzme različite položaje u prostoru uzimajući u obzir diskretizaciju radnog prostora. Međutim, u konkretnom zadatku, od robota se zahteva da dođe u položaj koji se u opštem slučaju ne poklapa sa nekim od diskretizacionih položaja. Primer za koor­dinatu q, prikazan je na slici 8.2b.  Traženi položaj qjf nalazi se između dve diskvetizacione tačke koje upravljački sistem može definisati. Tačnost pozicioniranja pretstavlja odstupanje koordinate od qjf . Očigledno da je gornja granica ovog odstupanja jednaka polovini prostorne rezolucije uvećane za poluinterval mehaničke nepreciznosti.

 

8.1.3. Tipovi upravljanja

 

Posmatrajući izvršni (servosistemski) nivo upravljanja možemo uočiti dva osnovna tipa upravljanja koji su tesno vezani i za tipove postavljenih zadataka. U pitanju su:

 

upravljanje od tačke do tačke, i

upravljanje kontinualnim kretanjem.

 

Upravljanje od tačke do tačke (engl. point-to-point control) podrazumeva da se robotu zadaje niz različitih položaja, te on mora redom da dođe u svaki od njih. Pri tome, način kretanja između dva zadata položaja nije bitan. Uprošćeno, zadatak se svodi na to da svaki zglob robota ("j"), polazeći od proizvoljnog položaja, postigne zadatu poziciju qjf sa odgovarajućom tačnošću.

 

Ovakvim načinom upravljanja mogu se rešiti mnogi zadaci u industrijskoj primeni robota, na primer tačkasto zavarivanje, prenošenje materijala i sl.

 

Upravljanje kontinualnim kretanjem (engl. continuons path control) pod­razumeva da robot prati zadatu putanju u prostoru uz zadatu promenu brzine duž putanje. Svedeno na servosistemski nivo, zadatak formulišemo u vidu zahteva da svaki zglob ("j") prati, sa određenom tačnošću, zadatu (nominalnu) promenu qjnom(t).

Ovakav način upravljanja neophodan je za izvršavanje zadataka kao što su: šavno zavarivanje, farbanje, pisanje i sl.

 

S obzirom na to da je ovaj drugi tip upravljanja opštiji problem, mi ćemo se pretežno koncentrisati na njegovo rešenje. U principu, upravljanje od tačke do tačke možemo posmatrati kao upravljanje kontinualnim kretanjem, pri čemu je zadata nominalna putanja jednaka konstanti tj. qjnom(t) =qjf, a početni položaj posmatramo kao početno odstupanje od zadate putanje.

 

8.2. UPRAVLJANJE RASPREGNUTIM SISTEMOM

 

Kada govorimo o upravljanju robotom kao raspregnutim sistemom, mislimo na to da se svakim zglobom robota upravlja kao izolovanim dinamičkim sistemom, dakle zanemarujući dinamički uticaj kretanja jednog zgloba na kretanje drugog. Razlog za ovo leži u složenosti proračuna dinamičkog sprezanja i težnji ka jednos­tavnosti upravljanja. Razmotrićemo mogućnosti ovakvog rasprezanja sistema.

 

U glavi 4. izveli smo dinamički model kompletnog robotskog sistema. Model smo doveli do kompaktne forme izražene jednačinom (4.23). Ovde ćemo se podsetiti da se kompletan model formira polazeći od modela dinamike motora i modela dinamike mehanizma.Dinamika motora zgloba "j" opisuje se jednačinom (4.15)

 tj.

 

:                                                               (8.1)

 

gde je xj vektor stanja podsistema motora "j" i dimenzija mu je kj. U daljem razmatranju usvojićemo kj=2, tj. ograničiti se na model drugog reda čiji vektor stanja sadrži položaj () i brzinu () motora:

 

xj = []T (8. 2)                                                                                      k

 

PMj je izlazni moment motora (skalama veličina), odnosno moment spoljašnjeg opterećenja, a uj je skalarni upravljački ulaz. Matrice sistema (Cj , fj , dj) opisane su u glavama 3. i 4.

 

Podsistemi SAj , j=l,...,n međusobno su spregnuti posredstvom dinamičkog modela mehanizma koji možemo napisati u formi (4.8). Ako pogone i kretanja zglobova povežemo sa pogonima i kretanjima odgovarajućih motora posredstvom reduktora odnosa Nj (relacija (4.16)), tada dinamiku mehanizma opisujemo mode­lom:

 

               (8.3)

 

Konkretno, podsistem SAj spreže se sa ostalim podsistemima kroz momenat opterećenja Pmj:

 

       (8.4)

 

Rasprezanje možemo najjednostavnije izvršiti na sledeći način. Koeficijente Hji, j≠i zanemarićemo tj. proglasiti ih nulama. Koeficijent Hjj koji predstavlja funkciju svih koordinata Θi, i=l,...,n smatraćemo konstantom i usvojiti vrednost Hjj koju dobijamo nekom vrstom usrednjavanja ili maksimizacijom. Konačno, sabirak hj(Θ,) takode ćemo smatrati konstantom čija je vrednost hj. Sada momenat opterećenja postaje

 

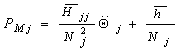                                                                      (8.5)

 

Na ovaj način podsistem SAj izolujemo od ostalih podsistema. Ukoliko Hjj/Nj2 dodamo inerciji rotora, tada model (8.1) postaje

 

SAj :                                                            (8.6)

 

Pri čemu C'j označava izmenjenu matricu Cj usled uvećanja momenta inercije.

 

Postavimo sada zahtev da koordinata Θj ostvari kretanje koje ćemo zvati nominalnim tj. Θjnom(t).Takvom kretanju odgovaraće promena brzine jnom(t). Kako raspolažemo senzorima koji mere položaj j i brzinu j , to praćenje nomi­nalnog kretanja realizujemo uvođenjem povratne sprege po koordinati i brzini j. Upravljački ulaz motora (uj) sastojaće se iz nominalne komponente ujnom(t) izračunate iz modela (8.6) za zadato nominalno kretanje i komponente povratne sprege ∆uj. Komponenta ujnom se često i izostavlja. Usvojimo daje ∆uj linearna funkcija odstupanja. Tada je:

 

∆uj = -KjP∆ Θj - KjD∆j                                                                      (8.7)

 

gde su:

 

∆ Θj = Θj – Θjnom                                                                                (8.8)

∆j = j -jnom                                                                                (8.9)

 

odstupanja položaja i brzine od nominalnih vrednosti, a KjP i KjD su pojačanja povratne sprege. Prvi sabirak u (8.7) nazivamo, obično, pozicionom povratnom spregom, a drugi brzinskom ili diferencijalnom spregom. Ukupno, ovaj način up­ravljanja nazivamo P-D regulatorom.

 

U modelu (8.6) uočavamo i sabirak fjhj/Nj koji predstavlja konstantni deo spoljašnjeg opterećenja. U takvom slučaju korisno je uvesti i integralnu povratnu spregu oblika KjI ∫∆Θjdt, zato što ova sprega ostvaruje upravljački signal čak i kada greška ∆Θj padne na nulu. Tako dolazimo do P-D-I regulatora

 

∆uj = -Kjp ∆Θj - KjD∆j - KjI∫∆Θjdt                                                 (8.10)

 

Način određivanja pojačanja povratne sprege (Kjp,Kjd,Kji) koja će obezbediti zadovoljavajuće praćenje nominalnog kretanja predstavlja zaseban problem. Moguće je koristiti bilo koju od standardnih metoda poznatih iz teorije automats­kog upravljanja, ali to već izlazi iz domena ove knjige.

 

8.3. DVOETAPNA SINTEZA UPRAVLJANJA

 

Glavni nedostatak pristupa upravljanju opisanog u prethodnom odeljku je potpuno rasprezanje sistema. Upravljanje sintetizovano na takvom raspregnutom modelu može biti u nekim slučajevima sasvim neprimerno realnom sistemu. Naime, nekada je sprezanje podsistema znatno i ne srne se na opisani način zanemariti.

U ovom odeljku pokazaćemo pristup koji u znatno većoj meri vodi računa o sprezanju.

 

Razdvojimo sintezu upravljanja na dve etape: etapu nominalnog kretanja i etapu poremećenog kretanja.

 

Smatraćemo da je zadatak dat u vidu traženog nominalnog kretanja robota koje je izraženo promenom unutrašnjih koordinata zglobova: qjnom(t),jnom, j=l,...,n. Kako su pomeranja motora direktno srazmerna pomeranjima zglobova, to pod nominalnim kretanjem podrazumevamo i Θjnom(t), jnorn{i), j=l,...,n. Ukoliko poznajemo dinamički model celog sistema (jednačine (8.1), (8.3) ili kompaktni mo­del (4.23), biće: ...(4.23)), ... tada možemo izračunati upravljanja ulnom(t), ...,unom (t) koja nazivamo nominalnim i koja će voditi sistem željenom putanjom. Ovaj proračun naziva se etapom nominalnog kretanja ili etapom nominalne dinamike.

 

Ukoliko robot izvršava neki zadatak u kome je kretanje Θjnom(t), j=l,...,n poznato pre početka izvršavanja, tada je moguće unapred rešiti nominalnu dina­miku i izračunato nominalno upravljanje ujnorn(t), j=l,...,n memorisati na nekoj od periferijskih jedinica kako bi se moglo čitati i koristiti prilikom izvršenja kre­tanja. Ovo je, uglavnom, slučaj kod rutinskih industrijskih primena robota kada se stalno ponavlja unapred dato kretanje. U nekom složenijem slučaju qjnom(t) pa otuda i Θjnom(t) dobija se od taktičkog nivoa ali u realnom vremenu, dakle u toku izvršenja. Tada i ujnom moramo računati u realnom vremenu, što podrazumeva da raspolažemo algoritmima za rešavanje dinamike u realnom vremenu.

 

Ako bismo na stvarni sistem primenili samo nominalno upravljanje, tada bismo dobili sistem sa otvorenom spregom koji ne bi mogao pratiti željeno kretanje. To je otuda što takav sistem nema osobinu samokorekcije. U tom slučaju, nakon bilo kakvog poremećaja koji ga izvede sa željene putanje, sistem će "odlutati". Dopunski razlog je što je i nominalno upravljanje samo približno onome što je realnom sistemu potrebno. To je otuda što dinamički model nikada ne može uzeti u obzir sve karakteristike realnog sistema.

 

Kretanje realnog sistema nazivamo etapom poremećenog kretanja i u toj etapi uvodimo povratne sprege i određujemo odgovarajuće komponente upravljanja: ∆uj , j=l,...,n. Ukupno, upravljanje će biti oblika:

 

uj = ujnorn+∆uj,   j=l,...,n,                                                                        (8.11)

 

ili vektorski:

 

u= unom + ∆u                                                                                          (8.12)

 

gde se pojavljuju vektori upravljanja (kolona matrice dimenzije n, npr u = [u1...un]T) Komponenta upravljanja usled povratne sprege (∆u), u principu, je funkcija odstupanja ∆Θ i ∆, gde je Θ vektor koordinata položaja motora (Θ= [Θ1...Θn]T). ∆u može biti još i funkcija vremena.

 

Sada ćemo podsetiti da je nominalno upravljanje sračunato na osnovu kompletnog modela dinamike, pa uzima u obzir sprezanje podsistema. Pri sintezi pov­ratne sprege, na etapi poremećenog kretanja, možemo sistem raspregnuti, ili se, pak, i dalje držati spregnutog modela. Prvi pristup nazivaćemo decentralizovano upravljanje, a drugi pristup pokazaćemo na primeru sinteze linearnog optimalnog regulatora.

 

8.3.1. Decentralizovano upravljanje

 

Ovaj pristup unekoliko sledi logiku rasprezanja izloženu u odeljku 8.2., me­đutim, ovde se radi o upravljanju koje na nivou nominala vodi računa o sprezanju, a kretanje oko nominala posmatra se raspregnuto.

 

Posmatraćemo model kompletne dinamike kao skup podsistema motora (8.1) koji su spregnuti posredstvom modela mehanizma (8.3). Kako nominalnu dinamiku smatramo rešenom, to nominalno kretanje i nominalno upravljanje smatramo poz­natim: Θ jnom(t),jnom{t), ujnom(t). U tom slučaju modele (8.1) i (8.3) možemo napisati u formi odstupanja od nominala. Tako za podsistem "j" dobijamo:

 

                                                            (8.13)

 

Gde je

 

∆xj = xj — xjnom(t),     ∆PMj = PMj - PMjnom',     ∆uj= uj – ujnom              k

 

a u slučaju modela drugog reda još i ∆xj = [∆Θj ∆ j]T.

 

Sprezanje ovog podsistema sa drugim podsistemima, na nivou poremećaja, vrši se posredstvom momenta ∆PMj. Kada model (8.3), odnosno (8.4) napišemo u formi odstupanja, dobija se:

 

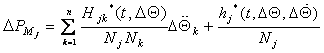                               (8.14)

 

gde je:

 

                                                                                               k

 

 (8.15)

 

a Θ označava vektor svih koordinata Θj.

 

Uočimo da kod pisanja u formi odstupanja svaka funkcija položaja Θ (npr. F(Θ)) postaje funkcija vremena t i odstupanja ∆Θ (npr. F(t, ∆Θ)) zbog toga što položaj posmatramo u obliku Θ=Θnom(t) + ∆Θ.

 

Jednačine (8.13) i (8.14), j = l,...,n određuju poremećajni model spregnu­tog sistema. Ukoliko želimo decentralizovano upravljanje, ovaj model je potrebno raspregnuti.

 

Prvo ćemo uočiti da se sprezanje podsistema "j'' (model (8.13)) sa ostalim podsistemima izražava kroz momenat ∆PMJ (8.14). U cilju rasrezanja, koeficijente H*jk, j≠k zanemarujemo. Zadržavmo samo H*jj i smatramo ga konstantom čija se vrednost određuje usrednjavanjem ili maksimizacijom.Označimo tu vrednost sa .Sabirak hj* možemo zanemariti ili smatrati linearnom funkcijom odstupanja ∆Θj , što se može proceniti prethodnom simulacijom. Ukoliko uvedemo  i zanemarimo hj*, iz (8.14) dobijamo:

 

                                                                      (8.16)

 

čime smo raspregnuli sistem.

 

Podsistem (8.13) sada postaje:

 

 = C'jxi + dj∆uj,                     (8.17)

 

pri čemu C'j označava izmenjenu matricu Cj usled toga što je moment inercije rotora uvećan za HJJ/Nj2.

 

Sinteza upravljanja Au} za sistem (8.17) sada se može izvršiti korišćenjem bilo koje od standardnih metoda (npr. metode postavljanja poslova). Određuju se pojačanja KjP i KjD i formira povratna sprega:

 

                                                            (8.18)

 

Ukupno upravljanje za podsistem "j" je:

 

                                                                          (8.19)

 

Očigledno je da se opisani način upravljanja razlikuje od pristupa izloženog u odeljku (8.2) prvenstveno po tome što je sada nominalno upravljanje izračunato iz spregnutog modela, dok je u prethodnom odeljku nominal računat iz raspregnutog modela, ili čak nije ni uziman u obzir.

 

Bez obzira na to što opisani postupak uzima u obzir sprezanje na nivou no-minala, sintetizovano upravljanje Uj ipak ne garantuje stabilnost realnog sistema u svim slučajevima. Kako je poremećeno kretanje posmatrano kao raspregnuto, to u slučajevima jakog sprezanja upravljanje može biti neodgovarajuće i čak dovesti do nestabilnosti. Možemo reći da su ovakvi slučajevi jakog sprezanja prilično retki, no ipak, nakon sinteze upravljanja, neophodno je proveriti stabilnost analizom ne­linearnog poremećenog modela (8.13), (8.14), j = l,...,n.

 

Upravljanje ∆uj sintetizovano na osnovu raspregnutog modela nazivamo lo­kalnom povratnom spregom. Ukoliko se na ovaj način stabilnost ne može postići, neophodno je uvesti dopunsku komponentu ∆ujG koju nazivamo globalnom pov­ratnom spregom i koja vodi računa o uticaju sprezanja.

 

8.3.2. Linearni optimalni regulator

 

Ovaj pristup suštinski se razlikuje od prethodnog po tome što se i u etapi poremećenog kretanja posmatra spregnuti sistem.

 

Pošto sistem nećemo rasprezati, to ćemo se pri izvođenju regulatora koristiti modelom kompletne dinamike napisanim u kompaktnoj formi (4.23) tj.

 

                                                                                (8.20)

 

gde je x vektor stanja celog sistema (dimenzija N), a u vektor upravljanja (dimen­zija n).

 

Ako kretanje razdvojimo na nominal xnorn(t) i odstupanje ∆x, tada model možemo napisati u formi:

 

∆x = C*(t,∆x) + D*(t, ∆x)∆u,                                                              (8.21)

 

gde je:

 

∆ = x - xnorn(t),   ∆u = u - unom(t);                                                        k

 

C*(t, ∆x) =  - + ;                  k

 

D*(t,∆x) = (x)                                                                                 (8.22)

 

Početno odstupanje ∆x(0) smatra se poznatim.

 

Izvođenje linearnog optimalnog regualatora zahteva niz složenih koraka (npr. linearizacija, rešavanje Rikatijeve jednačine, i sl.). Kako to prevazilazi obim ove knjige, to ćemo se na nekim mestima ograničiti samo na postavku problema i in­terpretaciju rezultata.

 

U cilju sinteze regulatora potrebno je linearizovati poremećajni model (8.21). Linearizacija se vrši oko nominalnog kretanja xnorn(t) tj. oko nule poremaćaja ∆x. Linearizacija se može izvršiti na različite načine: numeričkim metodama, sim­boličkim metodama ili, pak, metodama identifikacije. U postupke linearizacije ovde se nećemo upuštati. Naglasićemo, međutim, da se u svakom slučaju linearizovani model dobij a u obliku:

 

∆ = ∆x + ∆u,                                                                   (8.23)

  

gde se matrice  i  dobijaju linearizacijom i funkcije su vremena. Dakle, dobijeni linearni model je nestacionaran. Ako bismo sintetizovali optimalni regu­lator za takav sistem, došli bismo do vremenski promenljivih pojačanja povratne sprege. Kako je to u principu nepoželjno, izvršićemo uprošćenje modela (8.23) tako što ćemo ga usrednjiti tokom vremena, odnosno naći srednje vrednosti matrica  i  . Ako su srednje vrednosti  i , tada (8.23) postaje stacionarni model:

 

                                                                               (8.24)

 

Pretpostavimo sada da se sve koordinate stanja mere što omogućava da se povratna sprega uvede po svim odstupanjima ∆x, Tada sintezu regulatora vršimo na osnovu minimizacije kvadratnog kriterijuma.

 

                     (8.25)

 

gde su Q i R pozitivno definitne težinske matrice odgovarajućih dimenzija (Q(N x N); R(n x n)), koje se, kao i stepen stabilnosti γ, biraju tako da se obezbedi praktična stabilnost sistema.

 

Usvojeni postupak vodiće rešavnju Rikatijeve jednačine. Ukoliko upravljanje pretpostavimo u obliku:

 

                                                                      (8.26)

 

tada je K matrica dimenzija NxN i predstavlja rešenje Rikatijeve jednačine:

 

             (8.27)

 

gde je I jedinična matrica odgovarajućih dimenzija. Ukupno upravljanje je sada:

 

u = unom + ∆u.                                                                               (8.28)

 

Prilikom sinteze linearnog optimalnog regulatora uveli smo niz uprošćenja (linearizacija, usrednjavanje).Zbog toga rešenje (8.26) uz (8.28) ipak ne garantuje stabilnost realnog sistema. Zato bi trebalo izvršiti analizu stabilnosti nelinearnog modela poremećaja (8.21).

 

Dopunska nepogodnost leži u pretpostavci o merljivosti svih koordinata stanja i uvođenju povratne sprege po svakoj od njih. Naime, u praksi se, po pravilu, uvode povratne sprege samo po položaju i brzini motora. Na primer, ne uvodi se sprega po struji rotora iako je to jedna od koordinata stanja elektromotora (ako je opisan modelom trećeg reda).

                                          

8.4. DIGITALNA SHEMA UPRAVLJANJA

 

U prethodnim odeljcima izveli smo postupak upravljanja zasnovan na korišćenju nominalnog upravljanja i povratne sprege po položaju i brzini zglobova (q,). Preciznije rečeno, povratnu spregu smo uveli po položaju i brzini motora koji pokreću zglobove (dakle Θ,) S obzirom na jednoznačnu i prostu vezu između koordinata motora Θ i koordinata zglobova q, u principu je svejedno koja od ovih veličina će učestvovati u formiranju povratne sprege. Kako se u praktičnim realizacijama najčešće meri položaj i brzina motora, to smo u prethodnim odeljcima uveli odstupanje, pa i povratnu spregu po ovim veličinama (Θ,). Svakako, postoji i mogućnost merenja koordinate q umesto Θ (npr. ako se koristi potenciometar).

 

Prethodno razmatranje ipak nije u potpunosti tačno. Radi se o tome da u nekim slučajevima moramo uzeti u obzir elastične deformacije u sistemu za prenos pogona, a tada koordinate Θ i q postaju nezavisne (vidi odeljak 4.6). U takvom slučaju više nije svejedno da li se meri jedna ili druga veličina. Štaviše, u principu bi bilo poželjno meriti obadve,međutim,to bi nas vodilo specijalnim tipovima regulatora o čemu ovde nećemo govoriti.

 

Razmotrimo sada mogućnost praktične realizacije upravljačke sheme sa pov­ratnom spregom prikazane na sl.8.3.

 

Blok za izračunavanje ∆u na osnovu odstupanja ∆Θ i ∆ može se izvesti na različite načine, o čemu je govoreno u prethodnim odeljcima. Mi ćemo usvojiti da je u pitanju linearna forma tj.

 

                                (8.29)

 

 

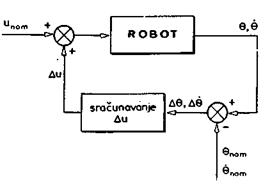
SI. 8.3.Upravljanje sa povratnom spregom

 

Ukoliko ovu shemu realizujemo digitalno, dolazimo do detaljnije sheme koja je prikazana na sl. 8.4. Pri formiranju ove sheme smatrano je da se nominal izra­čunava unapred, a u toku izvr­šenja zadatka čita se sa diska.

 

U nekom trenutku (t) senzori položaja mere koordinate Θ i .Nakon A/D konverzije po­daci ulaze u upravljački računar. Sada se sa diska čita vrednost nominalnog položaja Θnom(t) i brzine nom(t) i izračunavaju se greške ∆Θ= Θ - Θnom i ∆ =-nom

 

 Na osnovu tih grešaka formira se signal povratne sprege A«. Nakon sabiranja sa nominalnim upravljanjem (u = unom + ∆u) i D/A konverzije, dobijeni napon primenjujemo na motore.

 

Od trenutka očitavanja senzora, pa do trenutka primene upravljanja prošlo je izvsno vreme  ∆t. Dakle, upravljanje realizujemo ponavljajući opisani ciklus sa korakom ∆t koji nazivamo vreme razdvajanja. Dok se ne izračuna nova vrednost upravljanja primenjuje se vrednost izračunata u prethodnom koraku. Sledi da upravljanje ima stalnu vrednost tokom ∆t, a zatim se skokovito menja na novu izračunatu vrednost. Naglasimo još da u robotskim sistemima interval razdvajanja ne bi trebalo da bude duži od 20ms.

 

Pri primeni opisane sheme upravljanja uočavamo neminovno kašnjenje. Naime, upravljenje (u) koje odgovara stanju Θ,  tj. trenutku t, biće izračunato i primeniće se na motore tek u trenutku t + ∆t i vodiće motore sve dok ne stigne nova vrednost, a to je trenutak t+2∆t. Ovo kašnjenje, pogotovo u slučaju suviše velikog ∆t, može bitno uticati na kretanje robota. Ukoliko se pokaže potreba, ovo kašnjenje možemo korigovati postupkom predikcije (predviđanja).

 

Razmotrimo šta bi bilo neophodno uraditi u intervalu (t, t + ∆t) kako bi se korigovalo kašnjenje. Ako imamo u vidu da će upravljanje (u), izračunato u ovom intervalu, biti primenjeno tek od trenutka t + ∆t, onda zaključujemo da bi ono trebalo da odgovara tom trenutku,dakle u(t+∆t).

 

 Kako je nominalna komponenta smeštena na disk, to njenu vrednost unom(t + ∆t) možemo pročitati tokom intervala (t, t + ∆t). Međutim, povratna sprega ∆u(t + ∆t) zahteva poznavanje greški ∆Θ(t +∆t), ∆(t + ∆t), a to ne možemo izračunati budući da tokom intervala (t, t + ∆t) ne znamo položaj i brzinu koje će motori imati na kraju intervala (tj.Θ(t + ∆t) i (t + ∆t)). Da bismo opisanu ideju ipak sproveli izvršićemo predikciju i predvideti tražene vrednosti u trenutku t + ∆t na osnovu vrednosti u trenutku t (tj. na osnovu Θ(t), ( t)) i niza prethodnih vrednosti. Tako dobijamo prediktovane vrednosti Θ p i p koje koristimo za izračunavanje greški:

 

 i

 

Sam postupak predikcije ovde nećemo opisivati.

 

 

 

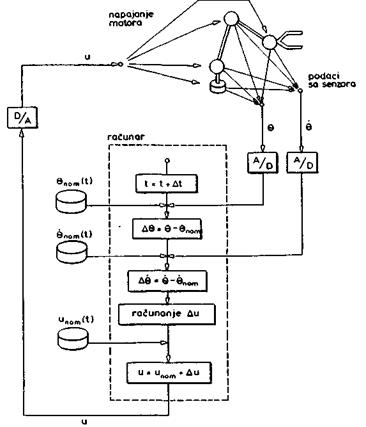
SI. 8.4. Digitalnu shema  upravljanja

 

Na slikama 8.3 i 8.4 uveli smo blok koji izračunava povratnu spregu ∆u u zavisnosti od greški ∆Θ i ∆. Pri tome smo rekli da se obično radi o linearnoj formi (8.29) tj. P-D ili P-D-I regulatoru.

 

Sa stanovišta realizacije najpovoljnije je da pojačanja povratne sprege (KP, KD, KI) budu konstantna. Međutim, u nekim slučajevima to nije moguće. Posmatrajmo, na primer, zadatak u kome robot prenosi neke predmete sa jednog mesta na drugo. U fazi nošenja robot (njegovi motori) je znatno više opterećen nego u fazi kada se prazan vraća. Dakle, menjaju se dinamički parametri, pa će jednoj fazi odgovarati jedne vrednosti pojačanja, a drugoj fazi druge vrednosti. Tako dolazimo do promenljivih pojačanja koja menjaju vrednost u određenim trenucima, ali su to poznate i zadate vrednosti izračunate unapred na osnovu poznatih tereta koji će biti prenošeni.

 

Složeniji problem nastaje ako robot prenosi terete koji nisu unapred poznati. Dakle, radi se o promeni dinamičkih parametara u obimu koji nije zadat. U takvim slučajevima primenjuju se postupci estimacije kojima se vrši procena vrednosti opterećenja, pa se na bazi toga određuju odgovarajuće vrednosti pojačanja povratne sprege. Kako se u ovom slučaju robot sam prilagođava novom teretu tj. izmenjenim dinamičkim parametrima, to govorimo o adaptaciji i adaptivnom upravljanju.

 

Međutim, ako promena dinamičkih parametara nije velika, tada nije neop­hodno menjati vrednosti pojačanja. Naime, pojačanja možemo već na početku odrediti tako da mogu odgovarati određenom intervalu promene nekog dinamičkog parametra. Tada kažemo da je upravljanje robusno u odnosu na promenu tog parametra.

 

8.5. PLANIRANJE KRETANJA

 

Planiranje kretanja robota podrazumeva definisanje nominalnog funkcionalnog kretanja Xnom(t) koje odgovara izvršenju postavljenog zadatka.

 

U nekim slučajevima kretanje Xnom(t) jednoznačno je određeno samim zadat­kom. Kao primer može nam poslužiti zadatak brušenja duž konture nekog vara (sl. 10.24b). Putanja je određena samom konturom, a orijenatacija uslovom normalonsti. Profil brzine direktno sledi iz zahteva za ravnomernim brušenjem.

 

Složeniji problem, međutim, nastaje ukoliko postoji višeznačnost rešenja nomi­nalnog kretanja. Naime, u zadatku brušenja, u fazi kada robot iz početnog položaja prilazi mestu gde brušenje počinje, moguć je različit način kretanja Xnorn(t). Slično se događa uvek kada se postavlja samo zahtev krajnjeg položaja, a do tog položaja kretanje se može proizvoljno birati. Još ozbiljniji problem javlja se u slučaju kada robot mora da stigne u određeni broj tačaka, a redosled nije zadat. Tada ne samo da se bira putanja između tačaka već i redosled.

 

Konačno, složen problem izbora kretanja javlja se u slučaju kada je potrebno da robot izbegne prepreke u radnom prostoru. Pri tome ne samo da hvataljka mora zaobići prepreku već ni bilo koji deo ruke ne srne da udari u prepreku.

 

Ceo opisani skup problema i načina za njihovo rešavanje naziva se planiranjem kretanja. Planiranje se, u principu, vrši na strategijskom nivou upravljanja i često uključuje različite postupke optimizacije.

 

Problematika planiranja kretanja prilično je složena i raznovrsna sa stanovišta pitanja koja obraduje. Zato ćemo se zadovoljiti time što smo naznačili probleme kojima se ova oblast bavi.

 

8.6. SIMULACIJA KRETANJA ROBOTA

 

Pri projektovanju robota i to kako mehaničke konstrukcije tako i upravljačkog sistema postavlja se problem određivanja čitavog niza važnih parametara. Kod me­haničke konstrukcije u pitanju su, na primer, dimenzije poprečnih preseka segme­nata mehanizma, a kod upravljačkog sistema može se raditi, na primer, o određi­vanju vrednosti pojačanja povratne sprege. Postoje različiti načini za određivanje ovakvih parametara. Međutim, vrednost izračunata ma kojim načinom ne može se smatrati verodostojnom dok se ne izvrši provera. Zadržimo se sada na ovom problemu provere. Provera podrazumeva analizu ponašanja realnog uređaja koji je napravljen na osnovu izračunatih vrednosti parametara. Zato je neophodno razviti postupak kojim bi se unapred, pre nego što je uređaj napravljen, moglo analizirati njegovo ponašanje. Takav postupak naziva se simulacija ponašanja.

 

Simulacija ponašanje robota zasniva se na njegovom matematičkom modelu. Umesto realnog uređaja koristi se matematički model čijim rešavanjem izračunava­mo kretanje budućeg uređaja. Matematički model (dinamički model) robota opisan je u glavi 4. ove knjige, a rešava se pomoću računara. Tačnost izračunatog kretanja zavisi od tačnosti modela. Radi se o tome da matematički model nikada ne uzima u obzir sve dinamičke efekte. Na primer, model opisan u glavi 4, iako je veoma detaljan, ipak ne vodi računa o svim pojavama. Konkretno, u obzir nije uzeto trenje u zglobovima mehanizma. Simulacija nam samo daje približne odgovore o ponašanju budućeg uređaja ali treba znati da su izračunati rezultati veoma bliski ponašanju realnog uređaja.

 

Izložiće se postupak za simulaciju kretanja robota koji ima digitalni sistem upravljanja. Na početku se prvo razmotre podaci koje je potrebno zadati računaru da bi se izvršila simulacija. S obzirom na to da dinamički model zamenjuje realni uređaj, neophodno je zadati one podatke koji su potrebni za rešavanje dinamičkog modela, a to su: geometrija, mase i momenti inercije, podaci o motorima, i konačno, početno stanje robota. Takođe je neophodno znati i one podatke koji su potrebni za upravljanje robotom. Dakle, treba znati strukturu upravljačkog sistema uključujući vrednost pojačanja povratne sprege.

 

Objasnimo sada simulaciju robota čija je upravljačka shema prikazana na slici 8.4. Ova shema zahteva da se pre početka upravljanja sračunaju nominalne vred­nosti Θnom(t),nom(t) i unom(t). Isti proračun obavlja se i pre početka simulacije.

 

Za vreme simulacije upravljački deo sheme ostaje isti, a realni mehanizam ro­bota treba zameniti matematičim modelom. Tokom objašnjenja upravljačke sheme videli smo da nakon svakog vremenskog intervala ∆t upravljački računar uzima od senzora podatke o položaju i brzini. Posmatrajmo neki trenutak t. Nakon dobijanja podataka Θ i  računar izračunava upravljanje u(t) i primenjuje ga na pogonske motore.   Kako je za A/D konverziju i izračunavanje upravljanja potrebno vreme ∆t to će se izračunato upravljanje primeniti na motore tek u trenutku t + ∆t. U međuvremenu (od t do t + ∆t) primenjuje se upravljanje iz prethodnog trenutka tj. u(t -∆t)(u' na sl. 8.5a). U trenutku t + ∆t ponovo se uzimaju podaci od senzora i ponavlja ceo ciklus. Da bi se pri simulaciji realni uređaj zamenio dinamičkim modelom moramo pomoću tog modela izačunati vrednosti Θ i  u trenutku t + ∆t tj. izračunati ono što bi trebalo meriti senzorom na realnom uređaju. Potrebno je izvršiti numeričku integraciju dinamičkog modela na intervalu (t, t + ∆t) i dobiti Θ(t + At) i (t + At) polazeći od vrednosti Θ(t) i (t), a pri tome primenjujući konstantno upravljanje u'. Shema postupka simulacije prikazana je na slici 8.5a.

 

Na slici 8.5b prikazana je shema simulacije u slučaju upravljanja sa predikcijom.

 

 

 

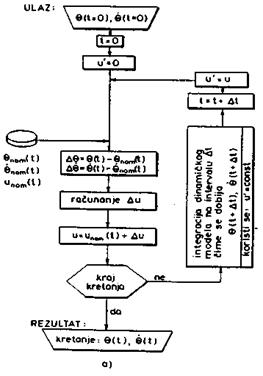
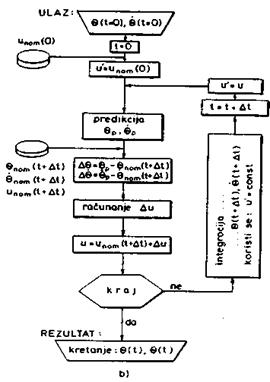
SI. 8.5. Shema postupka simulacije

 

Kao rezultat simulacije dobijamo od računara funkcije Θ(t) i (t)tj. zakon kretanja koje bi ostvario realni robot koji bismo napravili prema zadatim podacima. Treba reći da se početno stanje Θ(t0).(t0) može zadati tako da se uklapa u željeno kretanje, međutim, češće se zadaje tako da postoji neko odstupanje od željenog položaja u početnom trenutku. Ovo odstupanje uvodi se zato da bi se videlo kojom brzinom će izabrana upravljačka shema poništiti to odstupanje i dovesti robot na željenu putanju.

 

Sličnim postupkom može se pomoću računara izvršiti simulacija ponašanja robota koji ima bilo koju drugu strukturu upravljačkog sistema. Mogućnost simulacije ponašanja robota pruža velike šanse za usavršavanje procesa projektovanja. Moguće je brzo analizirati ponašanje velikog broja različitih konfiguracija robota radi izbora najpovoljnije. Moguće je i isprobati razne upravljačke sheme, razne vrednosti pojačanja itd.

 

8.7. PROGRAMIRANJE ROBOTA I  ROBOTSKI PROGRAMSKI JEZICI

 

U ovom odeljku, pod naslovom "programoranje robota" govorićemo o nešto široj problematici. Razmotrićemo mogućnost zadavanja zadatka industrijskom robotskom sistemu ili, još opštije, mogućnosti komunikacije sa takvim sistemom.

 

Ako posmatramo robota čiji upravljački sistem raspolaže izvršnim (servosistemskim) i taktičkim nivoom upravljanja, tada zadavanje zadatka podrazumeva specificiranje kretanja mehanizma robota i radnog režima završnog uređaja. Pod ovim drugim podrazumevamo npr. otvaranje i zatvaranje hvataljke, uključivanje i brzinu obrtanja uređaja za zavrtanje zavrtnja, uključivanje i isključivanje pištolja za prskanje boje i sl. Razmotrićemo različite mogućnosti za zadavanje ovakvog zadatka. Preciznije rečeno, radi se o postupcima kojima se robot osposobljava da izvrši traženi zadatak. Zato se često i koristi termin obučavanje robota.

 

U uvodnoj glavi knjige (glava 1) spomenuli smo neke prostije sisteme kao što su industrijski manipulatori kojima se kretanje određuje mehaničkim graničnicima ili uz pomoć prekidača. Svaka izmena kretanja zahteva pomeranje graničnika i takav postupak samo uslovno možemo zvati programiranjem kretanja. Kod nešto složenijih sistema, robota prve generacije, kretanje se zadavalo u obliku niza tačaka pri čemu je svaka od njih određena tj. "pamćena" uz pomoć skupa potenciometara. Svaki potenciometar pamtio je položaj jednog zgloba i to u obliku analogne napon­ske informacije. Mi ćemo se, međutim, u ovoj glavi posvetiti savremenim načinima obučavanja robota i zadavanja manipulacionog zadatka.

 

Kod savremenih industrijskih robota srećemo dva osnovna načina programi­ranja kretanja:

programiranje vođenjem,

tekstualno programiranje.

 

Ova dva načina, međutim, ne treba razdvajati kao dva potpuno različita kon­cepta koji se međusobno isključuju. Oni se često dopunjuju da bi se iskoristile prednosti svakog od njih.

 

8.7.1. Programiranje vođenjem

 

Ideja ovog pristupa je da se u fazi obučavnja robot vodi putanjom koja se zahteva pri izvršenju zadatka. Tada robot pamti izvršeno kretanje i ponavlja ga kada se to od njega zahteva tj. u fazi praktičnog rada.Ovo je bila osnovna ideja, dakle obučavanje pokazivanjem, međutim pri realiza­ciji ovog pristupa pojavljuje se niz razlika. Tako, prema načinu vođenja razlikujemo ručno vođenje i posredno vođenje.

 

Ručno vođenje podrazumeva da čovek-operator ručno vodi završni uređaj ro­bota onako kako on u praktičnom radu treba da se kreće. Pogodan primer je problem farbanja prskanjem. U fazi obučavanja operator pištoljem koji je učvršćen na vrhu robota radi one pokrete koje bi radio i pri ručnom farbanju. Na taj način on vodi robot koji kretanje pamti i tako se vrši obučavanje. Tokom ručnog vođenja operator uključuje i isključuje završni uređaj (npr. pištolj za prskanje) što robot takođe pamti.

 

U slučaju da je robot masivan i nepogodan za ručno vođenje projektuje se poseban mehanizam čija je geometrija identična sa geometrijom robota ali su mase značajno manje. Sada u fazi obučavanja operator ručno vodi ovu laganu "kopiju" robota.

 

Posredno vođenje je savremeniji način programiranja robota. Robot se kreće sledeći komande koje čovek-operator zadaje pomoću jedne vrste daljinskog uprav­ljača (najčešći engleski termin je: teach pendant). Na ovom uređaju za obuku, koji je oblika kutije i veličine šake, nalaze se prekidači i dugmad kojima se upravlja radom robota (sl. 8.6). Način vođenja posredstvom ovog uređaja bitno je vezan sa sledećom diskusijom.

 

 

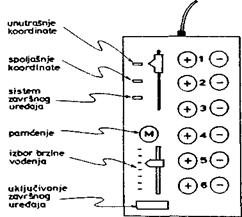
Sl.8.6 Uređaj za obuku

 

 Prema razmatranjima u glavi 2(geometrija i kinematika) jedan od načina za zadavanje položaja i kre­tanja robota je korišćenje unutrašnjih koordinata tj. pomeranja u zglobo­vima (sl. 8.7al). Ako želimo da obučavamo robot na ovaj način, tada ćemo na uređaju za obuku uočiti pre­kidač za izbor koordinata i posta­viti ga u položaj "unutrašnje koordi­nate" . Za vođenje robota koristićemo šest parova dugmadi1. Svakim parom dugmadi vodimo po jedan zglob ro­bota. Pritiskom na dugme "+" zglob se obrće u pozitivnom smeru, a pritis­kom na dugme "-" u negativnom. Na ovaj način, vođenjem jednog po jed­nog zgloba, dovešćemo završni uređaj u položaj koji se zahteva.Taj položaj robot će zapamtiti kada se na uređaju za obuku pritisne određeno dugme ili se, pak, na tastaturi upravljačke jedinice otkuca odgovarajuća naredba za pamćenje.                                 

 

Sada robot vodimo do drugog položaja koji se pamti, a postupak se ponavlja dok se u potpunosti ne definiše zadatak. Brzina vođenja može se podešavati posebnim regulatorom. Uključivanje i isključivanje završnog uređaja zadaje se pomoću odgo­varajućeg prekidača na uređaju za obuku ili, pak, kucanjem naredbe na tastaturi upravljačke jedinice.

 

U fazi izvršenja zadatka robot se kreće od jednog do drugog zapamćenog položaja pri čemu brzina nije određena brzinom vođenja tokom obuke, već se zadaje proizvoljno korišćenjem tastature. Pri kretanju od jednog do drugog zapamćenog položaja robot pokreće sve zglobove istovremeno.

 

 

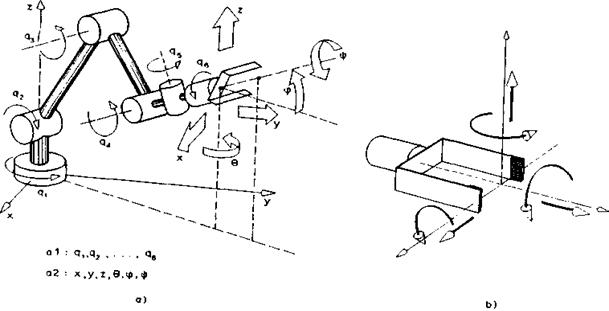
SI. 8.7. Način vođenja robota.

 

Drugi način definisanja položaja i kretanja robota je korišćenje tzv. spoljašnjih koordinata (sl. 8.7a2). U pitanju su tri Dekartove koordinate "vrha" završenog uređaja (x, y, z) i tri ugla koji određuju njegovu orijentaciju u prostoru (Θ,φ,ψ). Ako želimo da robot vodimo na ovaj način, tada prekidač za izbor koordinata stavljamo u položaj "spoljašnje koordinate". Šest parova dugmadi na uređaju za obuku sada dobija drugačije značenje. Pritiskanjem nekog dugmeta prvog para ("+" ili "-") menja se koordinata x, a sve ostale (y, z, Θ, φ ,ψ) ostaju konstantne. Tako se svakim parom dugmadi podešava po jedna spoljašnja koordinata dok se završni uređaj ne dovede u traženi položaj koji se tada zapamti.

 

Očigledno je da vođenje robota u spoljašnjim koordinatama zahteva rešavanje inverznog zadatka kinematike i to u realnom vremenu.

 

Treći način vođenja robota u fazi obučavanja je korišćenje koordinatnog sistema vezanog za završni uređaj (sl. 8.7b). Tada se kretanje ostvaruje u obliku translacija duž osa ovog sistema i rotacija oko tih osa. Svakako, opet se koristi istih šest parova dugmadi pri čemu se prekidač za izbor koordinata postavlja u položaj "sistem završnog uređaja".

 

Razmotrimo sada tipove upravljanja. Ukoliko zadatak zahteva upravljanje od tačke do tačke (bez zadatog kretanja između) tada je obučavanje moguće izvršiti i ručnim i posrednim vođenjem. Takvi su, na primer, zadaci prenošenja, zadaci opsluživanja mašina, tačkasto zavarivanje i sl.

 

Kada je u pitanju praćenje kontinualne putanje, tada je problem obučavanje složeniji. Krenimo od jednog jednostavnijeg slučaja iz ove kategorije. Zahtevamo da se završni uređaj kreće pravolinijski između dve tačke. Obučavanje se u ovakvom slučaju može efikasno realizovati posrednim vođenjem. Naime, sistem za obučavanje koji raspolaže mogućnošću rešavanja inverzne kinematike, po pra­vilu, uključuje i metodu prostorne pravolinijske interpolacije između dve zapamćene tačke.

 

Najsloženiji problem predstavljaju zadaci u kojima završni uređaj mora da ostvari neko krivolinijsko prostorno kretanje sa istovremenom promenom orijenta­cije. Današnji uređaji za posredno vođenje uglavnom ne omogućavaju da se završni uređaj vodi na ovakav način. Uređaj koji bi to omogućio očigledno bi morao biti opremljen nekom vrstom složene upravljačke palice, no takvi uređaji još nisu u široj upotrebi. Otuda se u slučaju složenog krivolinijskog kretanja završnog uređaja još uvek koristi ručno vođenje u fazi obučavanja.

 

Istaknimo sada prednosti i nedostatke programiranja robota postupkom vod-jenja. Dve su glavne prenosti. Prva je jednostavnost: ne zahteva se nikakav složen softver kojim bi se upravljačka jedinica osposobila za obučavanje. Druga prednost je opet jednostavnost ali sa stanovišta preciznosti. Radi se o tome da ne moramo unapred znati tačne koordinate položaja u kojima završni uređaj obavlja neke ope­racije. Potrebno je samo znati "gde treba izvršiti operaciju", a merenje položaja se obavlja samim dovođenjem robota tj. završnog uređaja na odgovarajuće mesto.

 

Osnovna nepogodnost obučavanja vođenjem leži u nemogućnosti da se prog­ramiranje robota izvrši unapred. Naime, programiranje se može izvršiti tek kada se robot postavi na proizvodnu liniju. To međutim, predstavlja priličan gubitak vremena, pogotovo ako se proizvodnja obavlja u malim serijama.

 

8.7.2. Robotski programski jezici

 

Kada govorimo o tekstualnom programiranju kretanja robota, obično podra-zumevamo programski jezik pomoću koga čovek-operator komunicira sa robotom i zadaje mu manipulacioni zadatak.

 

Danas je u upotrebi čitav niz robotskih programskih jezika različitog nivoa složenosti i različite opštosti. Dok su neki jednostavniji prilagođeni određenim primenama, dotle složeniji jezici dostižu priličnu univerzalnost i mogu se koristiti za programiranje niza zadataka u robotici. Ovu prilično raznovrsnu problematiku izložićemo na sledeći način. Zamislićemo jedan robotski jezik (nazvaćemo ga FO-ROB) tako što ćemo poznati programski jezik opšte namene - FORTRAN dopuniti određenim naredbama i osobinama koje će ga napraviti robotskim jezikom. Jezik koji ćemo na ovaj način formirati imaće određene sličnosti sa nekim postojećim robotskim jezicima i to nekada po formi pisanja naredbi, a nekada i po njihovom smislu. Ipak, jezik koji ćemo opisati samo je jedan hipotetički robotski jezik čija  je svrha da ilustruje glavne karakteristike savremenih robotskih programskih jezika.

 

Konstantne i promenjljive tipa položaja. Jedna od osnovnih karakteristika robotskog jezika je mogućnost da pored uobičajenih tipova konstanti i promenljivih (celobrojne i realne), radi i sa konstantama i promenljivima tipa položaja. Ovakva konstanta sadrži u sebi sve informacije o položaju robota. S obzirom na to da se položaj određuje sa šest koordinata (npr. za robot sa šest stepeni slobode), to konstanta tipa položaja sadrži šest brojnih podataka.

 

Podsetimo se sada da je položaj robota moguće odrediti preko unutrašnjih (q) i preko spoljašnjih (X) koordinata. Otuda postoje dve vrste konstanti položaja. Oznaka:

 

#          INTER: 0.785, 0., 1.57, 1.1, 0.2, 0.31#

 

predstavlja konstantu položaja pri čemu INTER ukazuje da šest brojeva koji slede, razdvojeni zapetama, predstavljaju unutrašnje koordinate robota tj. q1 = 0.785, q2 = 0., q3 = 1.57, q4 = 1.1, q5 = 0.2, q6 = 0.31. S druge strane kod konstante:

 

#          EXTER: 1.52, 1., 1.4, 0.785, 0.2, 1.1#

 

oznaka EXTER ukazuje na to da šest brojeva koji slede predstavljaju spoljašnje koordinate robota tj. x=1.52, y=l., z=1.4, Θ = 0.785, φ = 0.2, ψ = 1.1. Podrazumeva se da su sve veličine izražene u SI sistemu jedinica (dužine u metrima, a uglovi u radijanima).

 

Promenljiva tipa položaja označava se nizom alfanumeričkih znakova, na primer A12. Pri tome, slično naredbi DIMENSION, koja se koristi za vektore i mat­rice, u ovom slučaju se na početku programa koristi naredba POSITION kojom se ukazuje da je neka promenljiva položajna (na primer POSITION A12).

 

Ako želimo da nekoj položanoj promenjivoj dodelimo određenu vrednost, tada pišemo naredbu:

 

Al = # EXTER: 0., 0.5, 0.8, 0., 1.57, 0.# ,

 

 a moguća je i naredba:

 

B2 = # EXTER: Hl, AC3, UR, STT, SA, SB # , gde su Hl, AC3,...   realne promenljive koje su definisane u programu pre ove na­redbe.

 

Kada na ovaj način zadajemo položaj robota srećemo se sa jednim značajnim problemom: potrebno je veoma precizno poznavati koordinate željenog položaja. Ovo u praktičnom radu može biti nepogodnost. Naime, u primeru opsluživanja mašine operator zna da radni predmet treba dovesti i spustiti na određeno mesto u mašini, međutim, on, po pravilu, na zna numerički tačne koordinate te tačke. Zato se programski jezici obično formiraju tako da mogu prihvatiti i podatke dobijene posrednim vođenjem robota. Sada se položaj zadaje na taj način što se robot dovodi u željenu tačku, a zatim kuca naredba:

 

HERE Al kojom se promenljivoj Al daje vrednost trenutnog položaja robota.

 

Naredbe za kretanje od tačke do tačke. Kretanje robota iz trenutnog položaja u položaj određen promenljivom Al zadaje se naredbom:

 

MOVE A1

 

Kod ove naredbe podrazumeva se da je kretanje do položaja Al bazirano na up­ravljanju od tačke do tačke, tj. međupoložaji nisu bitni. Ukoliko se, međutim, želi pravolinijsko kretanje do tačke Al, naredba glasi:

 

 MOVES Al.

 

Sada je potrebno precizirati i brzinu kretanja. U slučaju upravljanja od tačke do tačke pogodno je zadati vreme prelaska u novu tačku. U tu svrhu koristi se naredba TIME u obliku:

 

TIME 2.5 ili

TIME T u zavisnosti od toga da li vreme želimo tretirati kao konstantu (2.5s) ili kao realnu promenljivu (T). Naredba TIME odnosi se samo na naredbu MOVE koja sledi odmah iza nje, na primer:

 

TIME T

 

MOVE B2

 

Zadavanje brzine kretanja robota moguće je i na drugi način koji je posebno pogodan kada se kretanje posmatra u spoljašnjim koordinatama. Tada se nared­bom:

 

SPEED 0.8/1.57 odnosno

SPEED V/OMEG zadaje brzina vrha od 0.8 m/s i brzina promene ugaone orijentacije od 1.57 rad/s, odnosno brzine V i OMEG.

 

Brzina se može zadavati i relativno, u odnosu na neku osnovnu brzinu koja se automatski postavlja na početku programa. Tako naredba:

 

SPEEDR 70 definiše brzinu kao 70 procenata od osnovne brzine.

 

Brzina definisana naredbom SPEED ili SPEEDR važi sve do nove naredbe SPEED (ili SPEEDR), tj. odnosi se na sva kretanja koja se programski definišu između dve naredbe za brzinu.

 

Promenljive tipa putanje. Cesto je neophodno obezbediti kretanje robota kroz određeni broj tačaka. Takvo kretanje nazivaćemo putanjom. Razlikovaćemo dve vrste putanja. Prva vrsta definiše se određenim brojem tačaka između kojih se vrši interpolacija. Promenljiva koja predstavlja takvu putanju deklariše se na početku programa naredbom:

 

PATH P/5/ što znači da promenljiva P predstavlja putanju definisanu sa 5 razdvojenih tačaka. U programu se ovakva putanja zadaje na primer skupom naredaba:

 

P/l/ = Al

P /2/ = CA

P /3/ = B

P /4/ = A5

P /5/ = # EXTER: 0., 1.5, 1., 0., 0., 0. #

 

čime se zadaje svaka od tačaka koje definišu putanju. Zadavanje može biti preko položajnih promenljivih (Al CA, ...) ili preko konstanti (kao što je zadato P /5/).

Druga vrsta putanje je kontinualna i određena nizom vrlo bliskih tačaka. U tom slučaju interpolacija nije potrebna. Odgovarajuća promenljiva deklariše se na početku programa naredbom:

 

PATHC P.

 

Zadavanje ovakve putanje vrši se po pravilu uz korišćenje ručnog ili posrednog vođenja. Naredbom HE(re)PAT(h)0, tačnije naredbom:

 

HEPAT0 P otpočinje pamćenje putanje P, a naredbom:

 

HEPAT1 P se završava.

 

Kretanje duž putanje. Za kretanje duž putanje prve vrste koristi se naredba:

 

MOVEP ukoliko se želi interpolacija u unutrašnjim koordinatama, a:

MOVES P ukoliko se želi pravolinijska prostorna interpolacija. Radi dobijanja glatke putanje moguće je izvršiti i kružnu interpolaciju naredbom:

MOVER P. Tada se prva kružnica provlači kroz tačke P/l/, P/2/, P/3/, i robot prati tu pu­tanju.   Od tačke P/3/ do P/4/ robot prati novu kružnicu provučenu kroz P/2/, P/3/ i P/4/, a zatim se postupak kružne interpolacije ponavlja.

 

Praćenje putanje druge vrste zadaje se naredbom:

MOVEC P.

 

Rad završnog uređaja. Naredbe kojima se određuje rad završnog uređaja u priličnoj meri zavise od vrste uređaja. Univerzalnost naredaba se može postići jedino ako se komunikacija sa završnim uređajem svodi samo na uključivanje i isključivanje. Tada naredbom:

 

TOOL ON uključujemo završni uređaj (na primer: stiskanje hvataljke, uključivanje pištolja za prskanja, i sl.). Naredbom:

 

TOOL OFF uređaj se isključuje (širenje hvataljke, zaustavljanje tocila za brušenje i sl.).

 

Ako je robot opremljen hvataljkom, tada se umesto naredbi TOOL ON i TOOL OF obično koriste naredbe: CLOSEG i OPENG (CLOSED(ripper)) i OPENG(ripper)). Ove naredbe ne treba mešati sa FORTRAN-skim naredbama OPEN i CLOSE koje služe za rad sa datotekama.

 

Naredbe za rad sa završnm uređajem mogu biti i složenije. Na primer:

 

CLOSEG (DISTANCE = 20 MM) je zahtev da se hvataljka skupi do razmaka prstiju od 20 mm. Naredba:

 

CLOSEG (FORCE = 1.2) je zahtev da se ostvari sila hvatanja od 1.2 N.

 

U primeru prskanja boje naredba:

 

TOOL ON (TIME = 15) obezbeđuje da pištolj bude uključen u trajanju od 15 sekundi.

 

Konačno, u primeru brušenja naredba:

 

TOOL ON (SPEED = 3 KRPM, FORCE = 20) predstavlja zahtev da se tocilo okreće brzinom od 3.000 obrtaja u minuti i da se ostvari sila pritiska od 20 N.

 

Uočićemo da one veličine koje su izražene u SI sistemu jedinica ne zahtevaju specificiranje jedinica, dok veličine koje se zadaju u drugim jedinicama zahtevaju preciziranje jedinica (npr. MM i KRPM).

 

Senzorske informacije tretiraju se kao realne ili logičke promenljive. Ovo drugo se koristi u slučaju binarnih senzora.

 

Promenljive koje nose senzorsku iniformaciju mogu biti skalarne, vektorske ili matrične, u zavisnosti od karaktera senzora. Na primer, skalama promenljiva od-govaraće senzoru temperature, vektorska promenljiva šestokomponentnom senzoru sile, a matrična promenljiva površinskom senzoru sile.

 

Nakon što se pogodnim naredbama neka senzorska informacija očita i dodeli joj se određena promenljiva, stoji nam na raspolaganju niz FORTRAN-skih arit­metičkih i logičkih operacija kojima možemo izraziti uticaj senzorske informacije na dalji rad robota.

 

 

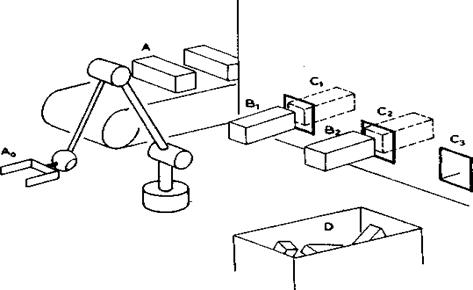
SI. 8.8. Shema manipulacionog zadatka.

 

PRIMER 1. Posmatrajmo jedan prost primer robotskog programa:

 

TIME 1.

MOVE# INTER: 0., 0., 1.57, 0., 0., 0.785 #

DT = 0.1

T = 2.

DO l I= 1,10

T1 = 2 * T/3

TIME T1

MOVE# INTER: 1.57,0.785, 2.355, 0., 0.785, 0. #

        T2 = T/3

       TIME T2

       MOVE# INTER: 0., 0., 1.57, 0., 0., 0.785 # 1        T=T - DT

 

Izvršavajući ovaj program robot će prvo iz svog trenutnog položaja preći u položaj q'= (0., 0., 1.57, 0., 0., 0.785) za vreme 1s. Zatim će 10 puta ponoviti ciklus kretanja iz položaja q' u položaj q"= (1.57, 0.785, 2.355,0., 0.785,0.) i natrag. Pri tome, vreme prelaska q'—+ q" je dva puta duže od vremena povratka q"—► q'.Vreme jednog ciklusa smanjuje se u svakoj iteraciji za O.ls, polazeći od 2s.

 

PRIMER 2. Na slici 8.8 prikazan je primer jednog manipulacionog zadatka. Pokretnom trakom dolaze predmeti koje je potrebno hemijski i termički ob­raditi. Robot kreće iz svog osnovnog položaja (Ao) i dolazi u položaj A gde hvata predmet. Sada sledi proces obrade. Robot donosi predmet u položaj B1, a zatim da pravolinijski uvlači u otvor C1 za nanošenje hemijskog sloja. Nakon 2 sekunde predmet se povlači natrag u B1. Zatim se pomera u B2 i onda pravolinijski uvlači u otvor C 2 gde ponovo ostaje 2 sekunde. Isto se ponavlja i sa otvorom C3, a nakon toga predmet se odlaže u kontejner D.

 

Programski segment kojim se definiše ovaj zadatak izgledao bi ovako:

 

SPEEDR 80    (podešavanje brzine)

MOVE A        (pokret u A)

CLOSEG        (hvatanje predmeta)

 MOVE B1      (pokret u B1)

        MOVES Cl         (uvlačenje predmeta u otvor Cl)

  STAY 2.        (robot stoji 2 sekunde)

 MOVES B1   (izvlačenje predmeta)

deo programa označen sa * ponavlja se analogno za otvore C2 i C3, nakon čega se robot našao u položaju B3

MOVE D        (pokret do kontejnera)

OPENG          (puštanje predmeta)

MOVE A0      (povratak u osnovni položaj gde robot čeka novi predmet).

 

Neke specifičnosti. Neki robotski jezici radi približavanja određenim praktičnim primenama, sadrže i veoma specifične naredbe. Karakterističan je sledeći primer: Robot često rešava zadatak hvatanja predmeta tako što prvo dovede hvataljku iznad predmeta na visinu, npr., 50 mm sa orijentacijom prema dole, a zatim hvataljku spusti i uhvati predmet. Ako položaj hvatanja označimo sa A, tada treba uvesti međutačku AA vertikalno iznad A za 50 mm. Program za definisanje ovog zadatka izgledao bi ovako:

 

MOVE AA

MOVES A

CLOSEG

MOVES AA

 

nakon čega se robot našao u međupoložaju odakle vrši dalje operacije sa predme­tom. Da bi se izbeglo zadavanje medupoložaja  AA uvodi se naredba APPRO A50 koja označava zahtev da hvataljka priđe tački A i postavi se na 50 mm iznad nje. Program bi sada izgledao ovako:

 

APPRO A50

 MOVES A

 CLOSEG

DEPART 50

 

gde naredba DEPART zahteva povratak hvataljke u medupoložaj iznad A.

 

Još jedna specifičnost je na primer naredba:

 

MOVE A VIA B

 

kojom se zahteva da robot iz trenutnog položaja dođe u položaj A ali da u tom kre­tanju prođe kroz B. Ovakvo zadavanje pokreta koristi se radi izbegavanja prepreke koja se nalazi između trenutnog položaja i položaja A.

 

Jedna od najvažnijih specifičnosti koje odlikuju najsavremenije robotske je­zike je mogučnost definisanja referentnih sistema ili, pak, mogućnost superpozicije položaja tj. uvođenje relativnog položaja. Posmatrajmo opet primer 2 iz ovog odeljka (sl.8.8): U tom zadatku zahtevano je uvođenje predmeta u tri otvora. Sam postupak uvođenja bio je identičan za svaki otvor ali se izvodi polazeći iz različitih položaja robota. Program je u primeru napisan tako da su tri puta ponavljane odgovarajuće naredbe. Jasno je da bi u slučaju većeg broja otvora ovakav način pisanja programa bio nefunkcionalan.

 

Jedan način za rešavanje ovog problema je definisanje referentnih sistema tako da svako uvlačenje bude zadato indentičnim skupom naredaba čime se omogućava formiranje programske petlje.

 

Drugi način postizanje istog cilja je uvođenje računskih operacija "sabiranja" i "oduzimanja" u skupu položajnih promenljivih. Pri ovome A+B se tretira kao superpozicija tj. B se smatra relativnim položajem u odnosu na A. Ova operacija naziva se i komponovanje. Kod oduzimanja, E=C-D daje relativni položaj C u odnosu na D.

 

Vratimo se primeru 2. i napišimo program koji koristi komponovanje i radi za K otvora. Uvedimo prvo promenljivu BB kao relativni položaj tačke B2 u odnosu na B1 i uopšte Bi+1 u odnosu na B .Takođe uvedimo promenljivu BC koja predstavlja relativni položaj Ci u odnosu na B. Položaj B1 zadaćemo u programu samo kao B. Sada program za zadatak u primeru 2. možemo napisati ovako:

 

SPEEDR 80

MOVE A

CLOSEG

DO 1 I=1,K

MOVE B

C=B+BC

MOVES C

STAY 2.

MOVES B

IF (I.EQ.K) GO TO 2

  B =B + BB

  MOVE D

OPENG MOVE A0

 

Ovim bismo kompletirali izlaganje o robotskim programskim jezicima smat­rajući da je to dovoljno da se shvate principi formiranja jezika.

 

Pri razmatranju upravljanja robotima niz problema je ostao nepotpuno ob­rađen. Na primer, nismo se upuštali u probleme sinteze lokalnih regulatora, nije obrađeno pitanje stabilnosti itd. U našem izlaganju o upravljanju prvenstveno smo obradili specifičnosti upravljačkih zadataka u robotici.